• 序列是Python中最基本的数据结构。序列中的每个元素都分配一个数字 - 它的位置，或索引，第一个索引是0，第二个索引是1，依此类推。
• Python有6个序列的内置类型，但最常见的是列表和元组。
• 序列都可以进行的操作包括索引，切片，加，乘，检查成员。
• 此外，Python已经内置确定序列的长度以及确定最大和最小的元素的方法。
• 列表是最常用的Python数据类型，它可以作为一个方括号内的逗号分隔值出现。
• 列表的数据项不需要具有相同的类型。
• 创建一个列表，只要把逗号分隔的不同的数据项使用方括号括起来即可。

如下所示：

list1 = ['Google', 'Runoob', 1997, 2000];
list2 = [1, 2, 3, 4, 5 ];
list3 = ["a", "b", "c", "d"];

与字符串的索引一样，列表索引从0开始。列表可以进行截取、组合等。

6.1、访问列表中的值

使用下标索引来访问列表中的值，同样你也可以使用方括号的形式截取字符，如下所示：

#!/usr/bin/python3

list1 = ['Google', 'Runoob', 1997, 2000];
list2 = [1, 2, 3, 4, 5, 6, 7 ];

print ("list1[0]: ", list1[0])
print ("list2[1:5]: ", list2[1:5])

以上实例输出结果：

list1[0]:  Google
list2[1:5]:  [2, 3, 4, 5]

6.2、更新列表

你可以对列表的数据项进行修改或更新，你也可以使用append()方法来添加列表项，如下所示：

#!/usr/bin/python3

list = ['Google', 'Runoob', 1997, 2000]

print ("第三个元素为 : ", list[2])
list[2] = 2001
print ("更新后的第三个元素为 : ", list[2])

注意：我们会在接下来的章节讨论append()方法的使用

以上实例输出结果：

第三个元素为 :  1997
更新后的第三个元素为 :  2001

6.3、删除列表元素

可以使用 del 语句来删除列表的的元素，如下实例：

#!/usr/bin/python3

list = ['Google', 'Runoob', 1997, 2000]

print ("原始列表 : ", list)
del list[2]
print ("删除第三个元素 : ", list)

以上实例输出结果：

原始列表 :  ['Google', 'Runoob', 1997, 2000]
删除第三个元素 :  ['Google', 'Runoob', 2000]

注意：我们会在接下来的章节讨论 remove() 方法的使用

6.4、Python列表脚本操作符

列表对 + 和 * 的操作符与字符串相似。+ 号用于组合列表，* 号用于重复列表。

如下所示：

Python 表达式	结果	描述
len([1, 2, 3])	3	长度
[1, 2, 3] + [4, 5, 6]	[1, 2, 3, 4, 5, 6]	组合
['Hi!'] * 4	['Hi!', 'Hi!', 'Hi!', 'Hi!']	重复
3 in [1, 2, 3]	True	元素是否存在于列表中
for x in [1, 2, 3]: print(x, end=" ")	1 2 3	迭代

6.5、Python列表截取与拼接

Python的列表截取与字符串操作类型，如下所示：

L=['Google', 'Runoob', 'Taobao']

操作：

Python 表达式	结果	描述
L[2]	'Taobao'	读取第三个元素
L[-2]	'Runoob'	从右侧开始读取倒数第二个元素: count from the right
L[1:]	['Runoob', 'Taobao']	输出从第二个元素开始后的所有元素

>>>L=['Google', 'Runoob', 'Taobao']
>>> L[2]
'Taobao'
>>> L[-2]
'Runoob'
>>> L[1:]
['Runoob', 'Taobao']
>>>

列表还支持拼接操作：

>>>squares = [1, 4, 9, 16, 25]
>>> squares += [36, 49, 64, 81, 100]
>>> squares
[1, 4, 9, 16, 25, 36, 49, 64, 81, 100]
>>>

6.6、嵌套列表

使用嵌套列表即在列表里创建其它列表，例如：

>>>a = ['a', 'b', 'c']
>>> n = [1, 2, 3]
>>> x = [a, n]
>>> x
[['a', 'b', 'c'], [1, 2, 3]]
>>> x[0]
['a', 'b', 'c']
>>> x[0][1]
'b'

6.7、Python列表函数&方法

Python包含以下函数:

序号	函数	描述
1	len(list)	列表元素个数
2	max(list)	返回列表元素最大值
3	min(list)	返回列表元素最小值
4	list(seq)	将元组转换为列表

Python包含以下方法:

序号	方法	描述
1	list.append(obj)	在列表末尾添加新的对象
2	list.count(obj)	统计某个元素在列表中出现的次数
3	list.extend(seq)	在列表末尾一次性追加另一个序列中的多个值（用新列表扩展原来的列表）
4	list.index(obj)	从列表中找出某个值第一个匹配项的索引位置
5	list.insert(index, obj)	将对象插入列表
6	list.pop([index=-1])	移除列表中的一个元素（默认最后一个元素），并且返回该元素的值
7	list.remove(obj)	移除列表中某个值的第一个匹配项
8	list.reverse()	反向列表中元素
9	list.sort( key=None, reverse=False)	对原列表进行排序
10	list.clear()	清空列表
11	list.copy()	复制列表

6.8、思考与总结

x = [[1,2,3]]*3
print(x)
x[0][1] = 20
print(x)

y = [1]*5
y[0] = 6
y[1] = 7
print(y)
上面代码运行结果是什么？为什么？

输出：

[[1, 2, 3], [1, 2, 3], [1, 2, 3]]
[[1, 20, 3], [1, 20, 3], [1, 20, 3]]
[6, 7, 1, 1, 1]

总结：

如果列表里面是复杂类型的值，那这个值很有可能是一个指针引用，修改这个值中间的某个元素，会改变其它的引用值

lst0 = list(range(4))
lst5 = lst0.copy()
print(lst5 == lst0)
lst5[2] = 10
print(lst5 == lst0)

输出：
True
False

lst0 = [1, [2, 3, 4], 5]
lst5 = lst0.copy()
lst5 == lst0
lst5[2] = 10
lst5 == lst0
lst5[2] = 5
lst5[1][1] = 20
lst5 == lst0

输出：
True

copy模块提供了deepcopy
import copy
lst0 = [1, [2, 3, 4], 5]
lst5 = copy.deepcopy(lst0)
lst5[1][1] = 20
lst5 == lst0

输出：
False

结论：通过对比，我们要引入一个概念，叫深浅拷贝，上述对比实验就是深浅拷贝，浅拷贝实际上相当于复制了一个指针，实际数据并没有复制，所以改或没改一定要落实到内存中数据本身，追踪内存中最本质的数据，才能运筹帷幄。那么，深拷贝就不言而喻了，指把数据本身也复制一份。

6.9、实例

6.9.1、求素数

用列表的方式求100000内的素数，基于的原理是“一个合数一定可以分解成几个素数的乘积，也就是说，一个数如果能被一个素数整除就是合数”

import datetime
start = datetime.datetime.now()
lst = [2]
count = 1
for i in range(3,100000,2):
    up = int(i**0.5 + 1)
    for j in lst:
        if i % j == 0:
            flag = False
            break
        if j >= up:
            flag = True
            break
    if flag:
        lst.append(i)
        count += 1
print(count)
delta = (datetime.datetime.now() - start).total_seconds()
print(delta)

6.9.2、杨辉三角实现

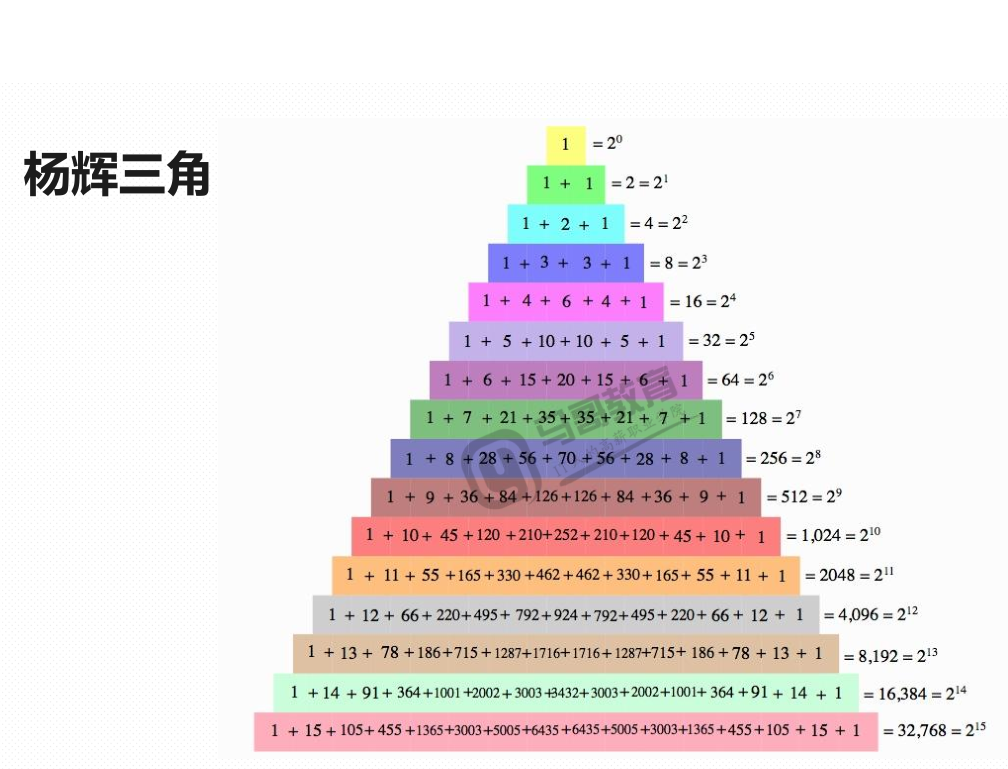
方法1：下一行依赖上一行所有元素，是上一行所有元素的两两相加的和，再在两头各加1

triangle = [[1],[1,1]]
n = int(input('please input line number: '))
for i in range(2,n):
    cur = [1] # 当前需要拼接的行
    pre = triangle[i-1] # 找到上一行
    for j in range(len(pre)-1):
        cur.append(pre[j]+pre[j+1]) # 相比较下面一种，cur作为临时列表，拼接完成后加入triangle
    cur.append(1)
    triangle.append(cur)
print(triangle)

方法1变种：下一行依赖上一行所有元素，是上一行所有元素的两两相加的和，再在两头各加1

triangle=[]
n = 6
for i in range(n):
    row = [1]
    triangle.append(row) # 这种方式的精髓就在于row作为一个复杂类型的变量嵌入列表中，row变化，列表随之变化
    if i==0:
        continue
    for j in range(i-1):
        row.append(triangle[i-1][j]+triangle[i-1][j+1]) # 所以数字追加直接在列表嵌套当中完成
    row.append(1)
print(triangle)

方法2：除了第一行以外，每一行每个元素（包括1在内）都由上一行的元素相加得到。如何得到两头的1呢？目标是打印指定的行，所以算出一行就打印一行，不需要用一个大空间存储所有已经算出的行。

n = int(input('please input line number: '))
newline = [1]
print(newline)

for i in range(1,n):
    oldline = newline.copy()    # 浅拷贝
    oldline.append(0)   # 在尾部加一个0，利用正负索引获取该0，算出第一个和最后一个1
    newline.clear()     # 以newline为容器算出当前行，算前清空

    offset = 0  # 初始化索引计算器
    while offset <= i:
        newline.append(oldline[offset-1]+oldline[offset]) # oldline是上一行列表，拼出当前行列表
        offset += 1
    print(newline)

输出：
please input line number: 4
[1]
[1, 1]
[1, 2, 1]
[1, 3, 3, 1]

方法2变种：除了第一行以外，每一行每个元素（包括1在内）都由上一行的元素相加得到。如何得到两头的1呢？目标是打印指定的行，所以算出一行就打印一行，不需要用一个大空间存储所有已经算出的行。

n = 6
newline = [1]
print(newline)

for i in range(1,n):
    oldline = newline.copy()    # 浅拷贝
    oldline.append(0)   # 在尾部加一个0，利用正负索引获取该0，算出第一个和最后一个1
    newline.clear()     # 以newline为容器算出当前行，算前清空

    for j in range(i+1):
        newline.append(oldline[j-1] + oldline[j])   # 当j为0时oldline[-1]索取0这一点比较巧妙；j>0时都是正索引，拼接当前行时好理解
    print(newline)

输出：
[1]
[1, 1]
[1, 2, 1]
[1, 3, 3, 1]
[1, 4, 6, 4, 1]
[1, 5, 10, 10, 5, 1]

方法3：前面2种在算法上不够优秀，主要是按部就班的方式拼凑，第3种方法主要有两个优化点

• 一次性开辟刚刚好的空间，利用乘法“*”一次性开辟，相较于append一个个追加要高效很多
• 利用对称性，只算一半，在算法高效上毋庸置疑

triangle = []
n = 6
for i in range(n):
    row = [1]*(i+1)     # i是从0开始的
    triangle.append(row)    # 精髓就在于row是一个引用类型，row改变，triangle中追加的row也会改变
# 循环的次数可以在草稿纸上画出来
# i == 0时，第1行，不需对称，无中点，不循环
# i == 1时，第2行，不需对称，无中点，不循环
# i == 2时，第3行，不需对称，有中点，循环1次    j == 1
# i == 3时，第4行，需要对称，无中点，循环1次
# i == 4时，第5行，需要对称，有中点，循环2次    j == 2
# i == 5时，第6行，需要对称，无中点，循环2次
    for j in range(1,i//2+1):   # i=2第三行才能进来，循环次数确定了
        val = triangle[i-1][j-1] + triangle[i-1][j]
        row[j] = val
        if i != 2*j:    # 根据上面找规律分析，当 i == 2*j 时，正好是中点，中点没有对称点，所以要跳过
            row[-j-1] = val # 对称点赋相同的值
print(triangle)

方法4：在方法3的基础上再进一步优化

• 只开辟一个列表实现

n = 6
row = [1]*n # 只开辟一次空间

for i in range(n):
    offset = n - i  # 对称填充时，从右向左定位用到的偏移量
    z = 1   # 用临时变量记录将要被覆盖的当前数值

    for j in range(1,i//2+1):   # i = 2时，也就是计算第三行时，才能进来
        val = z + row[j]    # 算出将要替换j位的数值
        row[j], z = val, row[j] # 替换j位数值，同时将j位原始的数值赋给z，用作计算下一位的值
        if i != 2*j:    # 只有奇数行才会出现 i == 2*j，这个位置正好是中间点，而中间点是没有对称点的，所以要跳过
            row[-j-offset] = val    # 每计算出一个左对称点，就找到右对称点进行对称赋值
    print(row[:i+1])    # 每一个 i 被 j 循环完，就可以截取 i + 1 个刚拼好的杨辉三角序列

6.9.3、杨辉三角n行k列求值

方法1：计算到m行，打印出k项

# 求m行k个元素
# m行元素有m个，所以k不能大于m
# 这个需求需要保存m行的数据，那么可以使用一个嵌套结构[[],[],[]]
m = 5
k = 4
triangle = []
for i in range(m):
    # 所有行都需要1开头
    row = [1]
    triangle.append(row)
    if i == 0:
        continue
    for j in range(1,i):
        row.append(triangle[i-1][j-1] + triangle[i-1][j])
    row.append(1)
print(triangle)
print("---------")
print(triangle[m-1][k-1])
print("---------")

测试效率：371 µs ± 8.43 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)

方法2：根据杨辉三角的定理：第n行的m个数(m > 0 且 n > 0)可表示为C(n-1,m-1)，即为从n-1个不同元素中取m-1个元素的组合数。

# 组合数公式：有m个不同元素，任意取n(n <= m)个元素，记作C(m,n)，组合数公式为：C(m,n) = m!/(n!(m-n)!)

# m 行 k 列的值，C(m-1,k-1)组合数
m = 9
k = 5
n = m - 1
r = k - 1
d = n - r
# C(m-1,k-1) = n!/(r!d!)
targets = []
factorial = 1
for i in range(1,n+1):
    factorial *= i
    if i == r:
        targets.append(factorial)
    if i == d:
        targets.append(factorial)
    if i == n:
        targets.append(factorial)
# print(targets)
print(targets[2]//(targets[0]*targets[1]))

测试效率：88 µs ± 2.57 µs per loop (mean ± std. dev. of 7 runs, 10000 loops each)

注：i == r、 i==n、 i==d 这三个条件不要写在一起，因为他们有可能两两相等。
算法说明：一趟到 n 的阶乘算出所有阶乘值。

6.9.4、排序

6.9.4.1、冒泡法排序

num_list = [[1,9,8,5,6,7,4,3,2],[1,2,3,4,5,6,7,8,9],[1,2,3,4,5,6,7,9,8],[9,8,7,6,5,4,3,2,1]]
nums = num_list[2]

print(nums)

length = len(nums)
count_swap = 0
count = 0

for i in range(length):
    flag = False
    for j in range(length-i-1):
        count += 1
        if nums[j] > nums[j+1]:
            tmp = nums[j]
            nums[j] = nums[j+1]
            nums[j+1] = tmp
            flag = True
            count_swap += 1
    if not flag:    # 目前冒泡排序优化点只能是刚刚好升序或者降序，也就是不发生交换，直接break出去
        break
print(nums, count_swap, count)

6.9.4.2、选择排序

m_list = [[1,9,8,5,6,7,4,3,2],[1,2,3,4,5,6,7,8,9],[1,2,3,4,5,6,7,9,8],[9,8,7,6,5,4,3,2,1]]
nums = m_list[1]
length = len(nums)
print(nums)

count_swap = 0
count_iter = 0

for i in range(length):
    maxindex = i
    for j in range(i+1,length):
        count_iter += 1
        if nums[maxindex] < nums[j]:
            maxindex = j
    if i != maxindex:
        nums[i],nums[maxindex] = nums[maxindex],nums[i]
        count_swap += 1
print(nums, count_swap, count_iter)

6.9.4.3、插入排序

m_list = [[1,9,8,5,6,7,4,3,2],[1,2,3,4,5,6,7,8,9],[1,2,3,4,5,6,7,9,8],[9,8,7,6,5,4,3,2,1]]
s_list = m_list[0]
sc_list = [0] + s_list # 待排序列最前面加一个位置给哨兵，这个位置必须要有，j -= 1 不能变成负值
count_swap = 0
count_iter = 0
for i in range(2,len(sc_list)): # 必须从待排序列的第2个数开始
    count_iter += 1
    sc_list[0] = sc_list[i] # 将循环到的数提到哨兵位置
    j = i - 1 # 从循环到的数前一位开始一一跟哨兵比较
    if sc_list[j] > sc_list[0]: # 加上这个判断，哨兵不用赋值到原来的位置上，多此一举
        while sc_list[j] > sc_list[0]:
            sc_list[j+1] = sc_list[j] # 比哨兵大，就右移
            j -= 1
            count_swap += 1
        sc_list[j+1] = sc_list[0] # 不比哨兵大，哨兵插入此值右边
print(sc_list[1:])
print(count_iter)
print(count_swap)

6.9.5、转置矩阵方阵

有一个方阵，左边方阵，求其转置矩阵

1 2 3       1 4 7
4 5 6 ==>   2 5 8
7 8 9       3 6 9

规律：对角线不动，a[i][j] <=> a[j][i]，而且到了对角线，就停止，去做下一行，对角线上的元素不动。

# 定义一个方阵
# 1 2 3       1 4 7
# 4 5 6 ==>   2 5 8
# 7 8 9       3 6 9
matrix = [[1,2,3],[4,5,6],[7,8,9]]
print(matrix)
count = 0
for i, row in enumerate(matrix):
    for j, col in enumerate(row):
        if i < j: # 这个条件是问题的关键所在，为什么是 i < j，可以手稿分析一下
            temp = matrix[i][j]
            matrix[i][j] = matrix[j][i]
            matrix[j][i] = temp
            count += 1
print(matrix)
print(count)

输出结果：
[[1, 2, 3], [4, 5, 6], [7, 8, 9]]
[[1, 4, 7], [2, 5, 8], [3, 6, 9]]
3

方法2：

matrix = [[1,2,3],[4,5,6],[7,8,9]]
length = len(matrix)
count = 0
for i in range(length):
    for j in range(i): # 这个循环很关键，正好通过边界控制取对角线以下的值，不包括对角线值
        matrix[i][j],matrix[j][i] = matrix[j][i],matrix[i][j]
        count +=1
print(matrix)
print(count)

输出结果：
[[1, 4, 7], [2, 5, 8], [3, 6, 9]]
3

总结：对称矩阵的诀窍存在于对角线，以上两种都是基于该方法实现，第2种更优秀，只循环一半。

6.9.6、转置矩阵非方阵

1 2 3          1 4
4 5 6   <==>   2 5
               3 6

方法1：扫描matrix第一行，在tm的第一列从上至下附加，然后再第二列附加，举例，扫描第一行1，2，3，加入到tm第一列，扫描第二行4，5，6，追加到tm第二列

# 定义一个矩阵，不考虑稀疏矩阵
matrix = [[1,2,3],[4,5,6]]
tm = []
count = 0
for row in matrix:
    for i,col in enumerate(row):
        if len(tm) < i + 1:
            tm.append([])
        tm[i].append(col)
        count += 1
print(matrix)
print(tm)
print(count)

输出结果：
[[1, 2, 3], [4, 5, 6]]
[[1, 4], [2, 5], [3, 6]]
6

方法2：能否一次性开辟目标矩阵的内存空间？如果可以，原矩阵的元素直接移动到转置矩阵的对称坐标就行了

matrix = [[1,2,3],[4,5,6]]
tm = [[0 for col in range(len(matrix))] for row in range(len(matrix[0]))]
count = 0

for i,row in enumerate(tm):
    for j,col in enumerate(row):
        tm[i][j] = matrix[j][i] # 将matrix的所有元素搬到tm中
        count += 1
print(matrix)
print(tm)
print(count)

输出结果：
[[1, 2, 3], [4, 5, 6]]
[[1, 4], [2, 5], [3, 6]]
6

6.9.7、数字统计

随机产生10个数字 。

要求：

• 每个数字取值范围[1,20]；
• 统计重复的数字有几个，分别是什么；
• 统计不重复的数字有几个，分别是什么；
• 举例：11，7，5，11，6，7，4，其中2个数字7和11重复了，3个数字4、5、6没有重复过。

思路：

• 对于一个排序的序列，相等的数字会挨在一起。但是如果先排序，还是要花时间，能否不排序解决？
• 例如 11，7，5，11，6，7，4，先拿出11，依次从第二个数字开始比较，发现 11 就把对应索引标记，这样一趟比较就知道 11 是否重复，哪些地方重复。
• 第二趟使用 7 和其后数字依次比较，发现 7 就标记，当遇到以前比较过的 11 的位置的时候，其索引已经被标记为 1，直接跳过。

import random

nums = []
for _ in range(10):
    nums.append(random.randrange(21))

print("Origin numbers = {}".format(nums))
print()

length = len(nums)
samenums = []
diffnums = []
states = [0] * length # 记录不同的索引异同状态

for i in range(length):
    flag = False
    if states[i] == 1:
        continue
    for j in range(i+1,length):
        if states[j] == 1:
            continue
        if nums[i] == nums[j]:
            flag = True
            states[j] = 1
    if flag:
        samenums.append(nums[i])
        states[i] = 1
    else:
        diffnums.append(nums[i])

print("Same numbers = {1}, Counter = {0}".format(len(samenums),samenums))
print("Different numbers = {1}, Counter = {0}".format(len(diffnums),diffnums))
print(list(zip(states,nums)))

结果输出：
Origin numbers = [8, 16, 14, 6, 15, 16, 20, 15, 9, 15]

Same numbers = [16, 15], Counter = 2
Different numbers = [8, 14, 6, 20, 9], Counter = 5
[(0, 8), (1, 16), (0, 14), (0, 6), (1, 15), (1, 16), (0, 20), (1, 15), (0, 9), (1, 15)]